시작하기 전에
거의 1년만에 작성하는 논문 리뷰다. 그 동안 논문을 보지 않은건 아니지만, 요즘 LLM을 사용하면서 글 쓰고 읽는 법을 잃어버린 사람이 되어버렸다. 앞으로는 스스로 작문하는 능력도 다시 키우고, 비교적 현대의 주요 논문들을 다시 한번 돌아보려 한다.
그래서 이제부터는 내 방식대로 논문을 리뷰하려고 한다. 배달 앱에 남기는 후기보다는 길고, 다른 리뷰 블로그들보다는 가벼울 것이다. 대신, 작문 과정에서 AI는 최대한 배제하고 내 생각을 담아보려고 한다. 인공지능을 전공하고, 연구 인턴도 했지만 내 본업은 인공지능 연구나 개발과는 거리가 있기 때문에 글은 자주 올라오진 않을 것 같다. (주말 내내 틈틈히 이 글을 적느라 너무 힘들었다)
아무튼 새로운 마음가짐을 한 기념으로 현대 최고의 논문 중 하나라 생각하는 Attention is all you need 논문을 리뷰하려고 한다. 이 논문의 인용 수만 봐도 1만건이 넘고, 2025년 Google I/O의 근본력이 어디서 나왔겠느냐? 라는 질문에 대한 해답이 되는 논문이라 생각한다.
- 원문 링크 : https://arxiv.org/abs/1706.03762
Background
사실 논문 리뷰를 찾아서 읽을 정도면 배경 지식은 충분히 있겠지만, 내 블로그까지 와서 볼 정도면 이미 다른 좋은 글들을 봐도 이해가 잘 되지 않았거나, 심심해서 들어와봤을 것이라 생각한다. 그러니 충분히 논문을 맛보기 위해 배경지식을 위한 문단 하나 정도는 괜찮지 않을까? (근데 쓰다보니 문단이 아니라 상당히 길어졌는데... 전공자라면 스킵 추천)
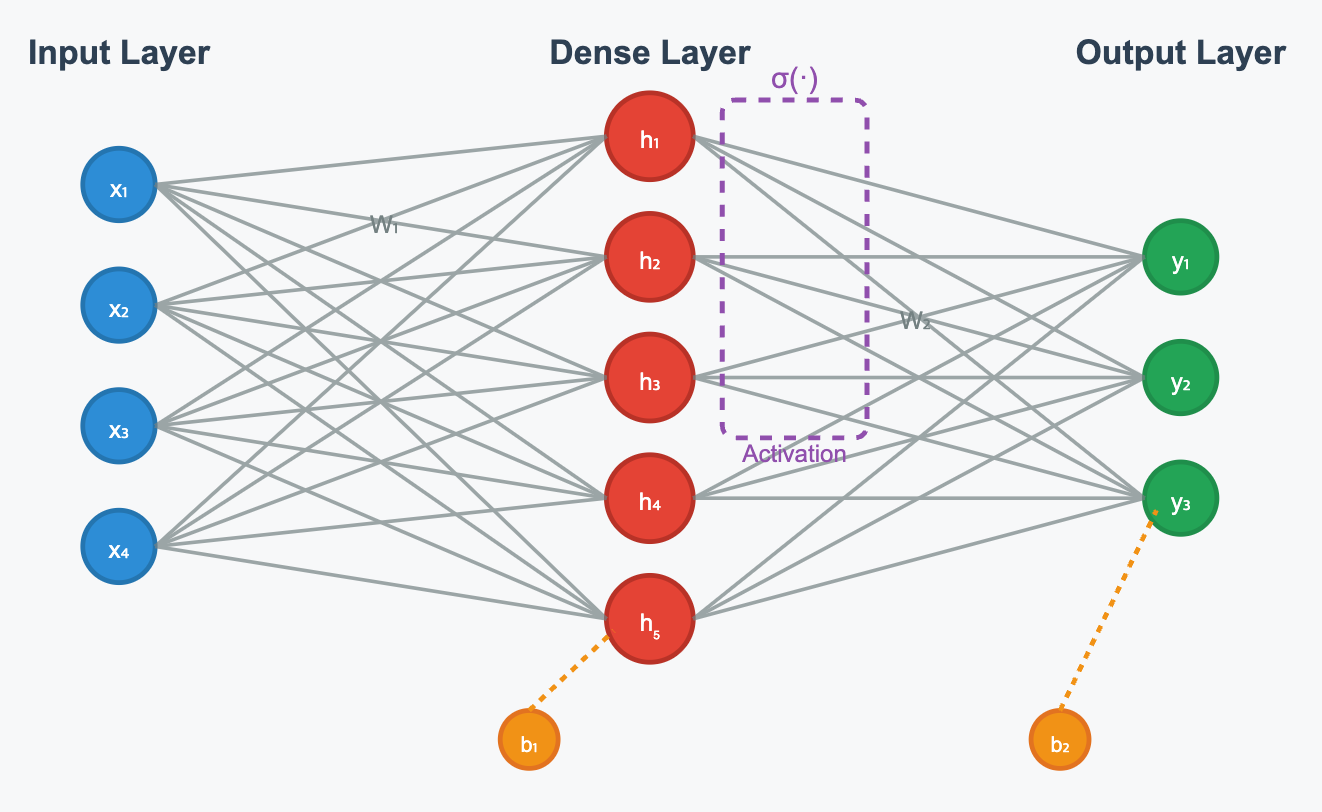
우선 딥러닝이 어떻게 동작하는지 간단히 알아보자. 우리가 흔히 접하는 Fully Connected Layer에서는, Input > Dense > Ouput 으로 데이터가 계산되고 학습된다. (순전파(입력 -> 출력 방향)로 기존에 있는 노드들의 값을 이용해서 계산하고, 역전파 (출력 -> 입력 방향)로 기존 노드 값들을 학습시킨다.)
위와 같은 과정이 선형적이라서 Linear layer라 부르고 여기에 활성화 함수를 추가하면 Deep Nerual Network (DNN) 이라 부른다. Dense Layer가 많을 수록 모델의 사이즈가 커지고, 계산과 학습에 있어서 많은 시간이 걸리고 이를 해결하기 위한 다양한 기법들을 소개하고 싶지만 일단 넘어가고, 이런 구조에서 수반되는 문제들을 해결하기 위해 수많은 석박들이 다양한 구조를 제안해냈다.
### RNN
그 구조 중에 RNN이 있는데, 선형 구조에서는 갖기 어려운 컨텍스트를 유지시키기 위해 개발되었다. RNN은 DNN이랑 비슷하니까 비슷한 구조라 생각할 수 있는데, 일부는 맞고 일부는 다르다. RNN은 크게 두 가지 특성이 있는데, output 값이 다시 input으로 반복된다는 특성과, 기억을 저장하기 위한 메모리인 Hidden State가 존재한다는 것이다.

처음 RNN을 접했을 때 가장 이해하기 어려웠던게 recurrent와 hidden state였는데, 사실 그렇게 어렵지 않다. RNN은 DNN의 다층 Layer 개념을 바로 대입하면 안된다. 일종의 시퀀스 데이터를 처리하기 위한 Cell에 가까운데 (이런저런 기능이 있는 복합적인) 다음과 같은 추론(계산) 절차가 이뤄진다.
1. 입력된 값을 RNN 내부의 가중치 행렬과 행렬 곱하여 계산한다.
2. 지난번에 출력된 값이 있다면, 그 값도 RNN 내부의 가중치 행렬과 행렬 곱하여 계산한다.
3. 그 두개를 합쳐서 Hidden State에 저장하고, 활성화 함수(tanh)를 거쳐서 출력한다.
예시를 하나 들어보면, 행복한 문장을 탐지하는 RNN에 "나는 어제 야근을 해서 피곤하다" 라는 문장을 토큰화 해서 주면 다음과 같은 순서대로 결과가 나온다. 이 경우, Many-to-One이라고 하는 마지막 결과값만 사용하는 방식이다. (더 궁금하면 다른 블로그를 찾아볼 것)
1. "나는" 입력 > 가중치 행렬을 통해 계산, 직전 출력 값은 없으니 기본 hidden state값 + bias를 합산해 hidden state에 저장
2. 활성화 함수를 통해 출력하고, 해당 값은 사용하지 않음 (다음 데이터 입력에만 사용)
3. "어제" 입력 > 가중치 행렬을 통해 계산하고, 기존 출력값도 가중치 행렬을 통해 계산
4. 계산된 두 값을 Hidden State에 저장하고, 활성화 함수를 통해 출력...
(마지막 토큰인 "피곤하다"까지 반복)
5. 최종 출력된 결과물을 이용하여 행복도 확인
이런 구조와 과정을 통해 시퀀스 데이터의 패턴을 RNN은 학습할 수 있게 된다. 이런 패턴이 많은 데이터일 수록 (자연어의 경우 단어 수준, 구문, 의미, 문맥 등등... 상당히 복잡하다.) Single Layer RNN으로는 해결하기 어렵고, 이를 해결하기 위해 Multi Layer RNN을 사용한다. (물론 어떤 레이어에 무엇을 학습하라고 지정하는건 불가능하다. 물론 간접적으로 가이드는 가능하다.)
참고로 Linear Layer는 가중치 행렬과 곱셈 + bias 를 수행하는 계층을 의미한다.
### LSTM/GRU
바로 위에서 자연어의 경우 상당히 복잡한 패턴을 가진다고 했는데, RNN Layer를 아무리 많이 쌓아도 문장이 길어지는 경우 초반 문장을 유지하기 어렵다. 그래서 등장한 것이 LSTM인데, RNN의 확장 개념이라고 생각하면 된다. LSTM의 큰 특징은 State를 두 개로 운영한다. (투배럭)

장기 기억을 위한 State는 Cell State라 부르고, 단기 기억을 위한 State는 Hidden State라 부른다. 그리고 정보를 처리하기 위한 Gate가 3개가 있는데, Cell State에서 잊을 정보를 결정하기 위한 Forget Gate, Cell State에 새로운 정보를 저장하기 위한 Input Gate, 그리고 Cell State에서 어떤 부분을 Hidden State로 출력할지 결정하는 Output Gate가 있다. (이미지에서 보이는 시그마가 gate 역할을 함)
위에서 했던 것처럼 계산 순서를 한번 살펴보자. 각 게이트에는 같은 값이 들어가기 때문에 계산하는 시점은 다를 수 있다.
1. 이번에 입력된 값과 이전 hidden state의 값을 합치고 Forget Gate, Input Gate에 집어넣는다.
2. Forget Gate에서는 Cell State에서 어떤 정보를 잊을지 결정한다.
3. Input Gate에서는 어떤 정보를 얼마나 받아들일지 결정한다.
4. 이번에 입력된 값과 이전 hidden state의 값을 가중치 행렬을 통해 선형 변환한 후, 활성화 함수(tanh)를 적용하여 candidate values를 계산한다.
5. Forget Gate의 결과 값을 이용하여 Cell State의 정보를 제거한다.
6. Input gate의 결과와 Candidate values를 곱해(element-wise) 새로운 정보를 생성한다.
7. 이전 정보가 제거된 Cell State의 값과 새로운 정보를 더해 Cell State를 업데이트 한다.
8. 이번에 입력된 값과 이전 hidden state의 값을 합치고 Ouput Gate에 넣어 출력할 정보를 결정한다.
9. Cell State의 값을 활성화 함수에 넣고, Output Gate에서 나온 값을 곱해(element-wise) hidden state를 다시 계산한다.
여기서 오해를 하면 안되는데, 각 게이트에서 나오는건 정보가 아니라 "비율" 이다. 각 차원의 값들을 얼마나 잊을지/유지할지/받아들일지에 대한 비율이다. 특정 차원의 값은 모두 잊을 수도 있고, 아니면 모두 유지하게 될 수도 있다.
보기만해도 일반 DNN에 비해 상당히 복잡한 구조를 가지고 있고, 실제로 모델 학습도 꽤 오래 걸린다. 이를 해결하기 위해 등장한 것이 GRU인데, 핵심 아이디어는 '굳이 State를 분리해야 하는가?' 에서 시작한다. 실제로 State를 하나로 줄였고, 하나로 줄였기 때문에 Input/Output Gate가 사라지게 되었고 Reset Gate와 Update Gate 두개로 운영한다.
각 게이트는 이전 정보를 잊는 비율 / 새 정보와 이전 정보의 비율을 결정하게 되고, 기본적인 동작의 흐름은 LSTM과 동일하니 길게 설명은 안해도 될듯.
###Attention (w/ Encoder, Decoder)
위에서 언급한 RNN/LSTM/GRU는 모두 공통적인 한계를 가지는데, 바로 시퀀스 처리의 한계이다. 문장의 모든 정보를 순차적으로 계산해서 마지막 state에 압축이 되는 구조인데, 아무리 LSTM이라 해도 정보 처리의 한계를 가질 뿐더러, 학습/추론 속도에도 문제가 생긴다.
이를 해결하기 위해 등장한 Attention 구조는 굳이 순차적으로 계산해서 압축할 필요가 있을까? 라는 물음의 해답이 되었는데, 어텐션은 모든 정보를 보존하고 있고 필요할 때 선택하는 구조로 동작한다. 그 전에 Encoder-Decoder 개념을 알아야 Attention 구조를 완전히 이해할 수 있는데 간단히 한번 알아보자.

사실 인코더/디코더로 파생되는 모든걸 이야기하면 이 글은 끝나지 않을 것이다. 간단하게, LSTM/GRU 셀을 여러개 붙여 놓고 입력을 받으면 인코더, 출력을 하면 디코더가 되는 셈이다. (사실 인코더, 디코더는 무조건 RNN으로 만들지 않아도 된다) 단, 이 과정에서 인코더는 입력 받은 값을 latent representation 해야 하고, 디코더는 이 표현을 원하는 형태로 출력하기만 하면 된다.
다만 학습/추론 과정이 좀 까다롭다. 훈련 시에는 지도학습을 하는데, 인코더에는 data가 들어가서 데이터 구조에 대한 학습을 하게되고, 디코더는그 context vector를 원하는 표현 (label)으로 출력하기 위한 학습을 한다. 이 과정을 통해 인코더는 context를 잘 추상화 할 수 있게 되고, 디코더는 추상화된 컨텍스트를 잘 표현할 수 있게되는 셈이다. 여기서 seq2seq의 인코딩, 디코딩 과정을 살펴보자.
Seq2Seq 인코딩
1. 첫 번째 단어를 인코더에 입력하고 첫 번째 hidden state를 계산한다.
2. 두 번째 단어와 첫 번째 hidden state를 합쳐서 인코더에 입력하고 두 번째 hidden state를 계산한다.
3. 이를 마지막 단어까지 반복한다.
4. 마지막 hidden state만을 Context Vector로 저장하고, 나머지는 버린다.
Seq2Seq 디코딩
5. Context Vector를 디코더의 초기 상태로 설정한다.
6. <START> 토큰과 Context Vector를 디코더에 입력하여 첫 번째 출력을 생성한다.
7. 첫 번째 출력과 고정된 Context Vector를 디코더에 입력하여 두 번째 출력을 생성한다.
8. 이를 <END> 토큰이 나올 때까지 반복한다.
9. 모든 시점에서 같은 Context Vector를 재사용한다.
자 여기까지는 우리가 위에서 알게된 LSTM/GRU 레이어가 합쳐져 있는 느낌과 매우매우 유사하다. 어텐션도 종류가 많지만, 우리가 알아야 할 어텐션은 dot-product attention이다. 아래 사진을 한번 살펴보자.

또 뭐가 많이 생겼다. 이번엔 hidden state마다 attention score를 계산하는게 추가되었는데, attention score는 현재 decoder와의 내적을 통해 유사도를 계산한다. 그리고 attention score를 softmax 레이어에 넣어 attention weight를 만드는데, 이 attention weight 덕분에 encoder와 decoder가 의미를 이해할 수 있게 되는 것이다.
왜냐하면, attention weight와 encoder의 hidden state를 다시 곱하고(element-wise) 가중합을 통해 동적 context vector를 생성하는데, 이를 decoder에 입력해서 첫 출력과 새로운 decoder 상태가 생성된다. 이 때 새 디코더의 상태와 인코더의 hidden state 간의 내적을 다시 계산하는데, 이를 통해 새로운 attention weight가 나오게 된다.
즉 모든 hidden state가 decoding에 참여하게 되고 context vector가 동적으로 변화하기 때문에, 기존 구조에서의 고정 context vector가 가지는 정보 손실 문제와 병목 현상이 해결된다. (다만 계산 복잡도는 늘어났다. 그건 어쩔 수 없는 숙명)
다시 한번 정리해보자.
Attention 인코딩
1. 첫 번째 단어를 인코더에 입력하고 첫 번째 hidden state를 계산한다.
2. 두 번째 단어와 첫 번째 hidden state를 합쳐서 인코더에 입력하고 두 번째 hidden state를 계산한다.
3. 이를 마지막 단어까지 반복한다.
4. 모든 hidden state들을 보존한다.
Attention 디코딩
5. 현재 디코더 상태와 모든 인코더 hidden state들 간의 내적을 계산해 attention score를 계산한다.
6. attention score를 softmax를 통해 attention weight로 변환한다.
7. attention weight와 인코더 hidden state들을 곱해서(element-wise) 가중합으로 동적 Context Vector를 생성한다.
8. <START> 토큰과 동적 Context Vector를 디코더에 입력하여 첫 번째 출력과 새로운 디코더 상태를 생성한다.
9. 새로운 디코더 상태와 모든 인코더 hidden state들 간의 내적을 다시 계산한다.
10. 새로운 유사도 점수들을 softmax를 통해 새로운 어텐션 가중치로 변환한다.
11. 새로운 attention weight와 인코더 hidden state들을 곱해서 새로운 동적 Context Vector를 생성한다.
12. 첫 번째 출력과 새로운 동적 Context Vector를 디코더에 입력하여 두 번째 출력과 디코더 상태를 생성한다.
이제 이 논문을 즐기기 위한 배경 지식은 모두 확보했다. self-attention을 기반으로 하는 transformer가 어떤 문제를 해결했을지 살펴보자.

Scaled Dot-Product Attention
Transformer는 scaled dot-product attention 구조를 제안한다. 기존 어텐션은 디코더 상태와 인코더 hidden state간의
유사도를 측정했지만, scaled dot-product attention에서는 같은 시퀀스 내에서 모든 위치끼리 계산할 수 있다. 즉, 시퀀스 내의 각 단어와 모든 단어의 내적을 계산하는데... 그래서 이름이 self-attention인 셈.
좀 더 구체적으로 이야기를 해보면, 현재 단어의 관점을 기록하게 되는 Query, 각 단어가 제공하는 정보의 식별자인 Key, 각 단어의 실제 정보인 Value를 생성하기 위한 가중치 행렬들이 등장한다. 어? Attention은 hidden state가 필요하지 않나요? 라는 생각이 든다면 이 글을 잘 읽은 것이다.
트랜스포머는 일반적인 Seq2Seq 구조와 다르게, RNN을 사용하지 않는다. 단어를 임베딩 벡터로 바꾸고, 그 다음 Query, Key, Value를 구한다음 Attention을 계산하게 된다. 이렇다는건... RNN의 무지막지한 연산을 하지 않아도 되어 엄청난 이점이 있다. (물론 현대의 모델은 또 다릅니다.)
그렇기 때문에, 현재 디코더 상태와 인코더 hidden state를 계산하던 Attention Score는 이제 현재 단어(Query)와 모든 단어(Keys)간의 내적을 통해 유사도를 계산하는 것으로 바뀐다.
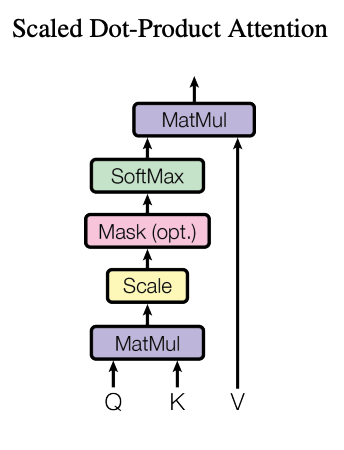
그리고, 이 계산한 값을 Key의 차원의 제곱근으로 나누어 스케일링한다. 왜냐하면, 키의 차원이 커질 수록 dot product의 값이 커지면서 softmax의 값을 saturated 하게 만들기 때문에 기울기가 소실되는 문제가 발생하기 때문이다.
쉽게 설명하면 softmax 함수의 특성을 고려했다는 뜻. 이후 스케일링이 끝난 값을 softmax 함수에 넣어서 Attention Weight를 만들고, 그 값을 Value와 행렬곱하고 가중합을 구하게 된다.
과연 RNN없이 동작하는 Transformer의 핵심인 Self-attention이 어떻게 동작하는지 다시 한번 살펴보자.
일반적인 Attention의 동작
0. 인코딩 동작이 완료되어 hidden state값이 도출된 상태.
1. 현재 디코더 상태와 모든 인코더 hidden state들 간의 유사도를 계산해 attention score를 계산한다.
2. attention score를 softmax를 통해 attention weight로 변환한다.
3. attention weight와 인코더 hidden state들을 곱해서 가중합으로 동적 Context Vector를 생성한다.
Self-Attention 동작
1. 단어를 임베딩 벡터로 바꾸고 Query, Key, Value 가중치 행렬과 행렬 곱하여 Q, K, V값을 계산한다.
2. Q와 K간의 내적을 계산하여 Attention Score를 계산한다.
3. Attention Score를 Key의 차원의 제곱근으로 나누어 scaled_score를 구한다.
4. scaled_score를 softmax를 통해 attention weight로 변환한다.
5. value와 attention_weight을 곱해(element-wise) 구해 출력을 구한다.
6. 출력과 예측값을 비교해 손실을 계산하고, 역전파를 통해 Query, Key, Value 가중치 행렬을 학습시킨다.
어텐션 동작에서도 큰 차이가 있는데, hidden_state 간의 가중합을 구하는 것과 value와 attention_weight의 가중합을 구하는 것은 엄청난 처리 속도의 차이가 있다. 기존 구조에서는 순차적으로 처리해야 했지만, 현재 구조는 병렬적으로 처리가 가능하다. (각각이 독립적)
또한 모델이 아주 커진다면, hidden_state가 엄청나게 커지는 문제가 발생한다. 그렇지만 value와 attention_weight의 가중합 계산은, "입력과 출력 사이즈"에만 성능에 영향을 준다.
우리가 현재 chatGPT와 claude를 사용하면서, 가끔씩 마주치는 '대화가 너무 길어서 종료되었습니다' 라는게 왜 발생하는지, 우리는 이제 근본적으로 알게 되었다. 이어서 Self-Attention 구조를 트랜스포머가 어떻게 활용하는지 살펴보자.
요약 : Self-Attention은 기존 Encoder와 Decoder 구조의 RNN을 Self-Attention구조로 대체해서 병렬 처리와 연산 속도의 이점을 얻었다.
Multi-Head Attention
아이고 머리야... 보기만해도 머리가 어지러워지는 이름이다. 근데 사실 쉽다. 셀프 어텐션(이하 어텐션)을 병렬로 만들었더니 효과가 좋더라~ 라는 내용이다. 위에서 RNN을 이야기할 때, RNN을 여러번 연결하면 각각의 셀들이 특정 패턴들만 집중해서 전체적으로 효과가 좋아진다고 했는데 그 개념을 Attention에도 차용했다. 다만 선형 구조가 아니라 병렬적인 구조로 동작한다. 심지어 계산 비용도 동일하다.

Single Head Self-Attention
# 1. Q, K, V 계산
Q = X @ W_Q # [n, 512] @ [512, 512] = O(n × 512²)
K = X @ W_K # [n, 512] @ [512, 512] = O(n × 512²)
V = X @ W_V # [n, 512] @ [512, 512] = O(n × 512²)
# 2. Attention Score
scores = Q @ K.T # [n, 512] @ [512, n] = O(n² × 512)
# 3. Softmax
weights = softmax(scores) # [n, n] = O(n²)
# 4. 최종 출력
output = weights @ V # [n, n] @ [n, 512] = O(n² × 512)
# 총 복잡도: O(3n × 512² + 2n² × 512 + n²)
Multi-head Self-Attention
# 1. Q, K, V 계산 (8개 헤드)
for i in range(8):
Qi = X @ W_Qi # [n, 512] @ [512, 64] = O(n × 512 × 64)
Ki = X @ W_Ki # [n, 512] @ [512, 64] = O(n × 512 × 64)
Vi = X @ W_Vi # [n, 512] @ [512, 64] = O(n × 512 × 64)
# 8개 헤드 총합: 8 × 3 × O(n × 512 × 64) = O(3n × 512²) ✅ 동일!
# 2. Attention Score (8개 헤드)
for i in range(8):
scores_i = Qi @ Ki.T # [n, 64] @ [64, n] = O(n² × 64)
# 8개 헤드 총합: 8 × O(n² × 64) = O(n² × 512) ✅ 동일!
# 3. Softmax (8개 헤드)
for i in range(8):
weights_i = softmax(scores_i) # [n, n] = O(n²)
# 8개 헤드 총합: 8 × O(n²) = O(8n²) ❌ 8배 증가!
# 4. Attention 출력 (8개 헤드)
for i in range(8):
head_i = weights_i @ Vi # [n, n] @ [n, 64] = O(n² × 64)
# 8개 헤드 총합: 8 × O(n² × 64) = O(n² × 512) ✅ 동일!
# 5. 최종 출력 변환 (추가!)
output = concat_heads @ W_O # [n, 512] @ [512, 512] = O(n × 512²)
# 총 복잡도: O(4n × 512² + 2n² × 512 + 8n²)
계산하기 귀찮아서 클로드한테 맡겼더니 잘 계산해 준 것 같다. 중간에 softmax가 8배 증가했지만, 저 친구는 지배항이 아니기 때문에 크게 영향을 미치지 않는다. 성능을 높이기 위한 아주 사소한 세금같은 것이라고 생각하자. (물론 절대적인 계산 자체도 늘어나는건 맞다. 다만, 시간 복잡도 자체가 변화하지 않는다는 것을 보여주기 위한 친절한 설명이므로 의문이 든다면 시간 복잡도를 검색해보자)
Multi Head Attention 동작
1. 각 헤드별로 Self-Attention의 학습 과정을 완료한다.
2. 헤드별 어텐션이 출력하는 값들을 모아서 선형으로 변환한다.
3. 최종 linear layer와의 행렬곱을 구해 출력한다.
그럼 우리는 여기서 한 번 생각해볼 수 있다.
그럼 학습시켜야 하는 양이 8배가 된 것 아닌가요?
맞다. 괜히 강조해보고 싶었다. 왜냐하면, 이전에 시키던 지도학습에 비해 label이 8배 더 필요해진거다. 이 빌드업은 아마 다음 게시글에서 이어보겠다.
그런데, 이 논문에서 제시하는 attention구조는 '순차적' 이지 않기 때문에 단어의 위치나 순서를 알 수가 없다. 그래서 이것을 해결하기 위해 디코더에 입력할 때 토큰 임베딩 데이터와 위치 인코딩된 값을 같이 넣어준다. 토큰의 위치를 임베딩 차원의 인덱스와 모델의 차원으로 나눠 sin, cos로 계산해서 넘겨준다. sin, cos구조에 의해 상대적인 위치 관계를 빠르게 얻을 수 있다는 점도 장점.
그리고 이 구조에서 디코딩은 autoregressive하게 동작하는데, 쉽게 설명하면 다음 단어를 추론해서 생성하고, 그 값을 다시 집어넣어서 다음 단어를 추론하는 구조라고 생각하면 쉽다. Background에서 설명했던 그런 느낌. 그대로 이어가면 된다.
요약 : Self-Attention의 장점은 다음과 같다.
- 시간 복잡도는 유지한 채, multi-layer 효과를 낼 수 있다.
- self-attention은 병렬적으로 연산이 가능하다.
- 단어의 위치를 디코더에 넣어주기 때문에, 컨텍스트가 길어져도 해석이 쉽다.
Transformer
논문에서는 실험을 위해 약간의 추가 처리를 하긴 했지만, 이제 우리는 트랜스포머의 구조에 대해 모두 이해했다. 아래 이미지를 살펴보자.
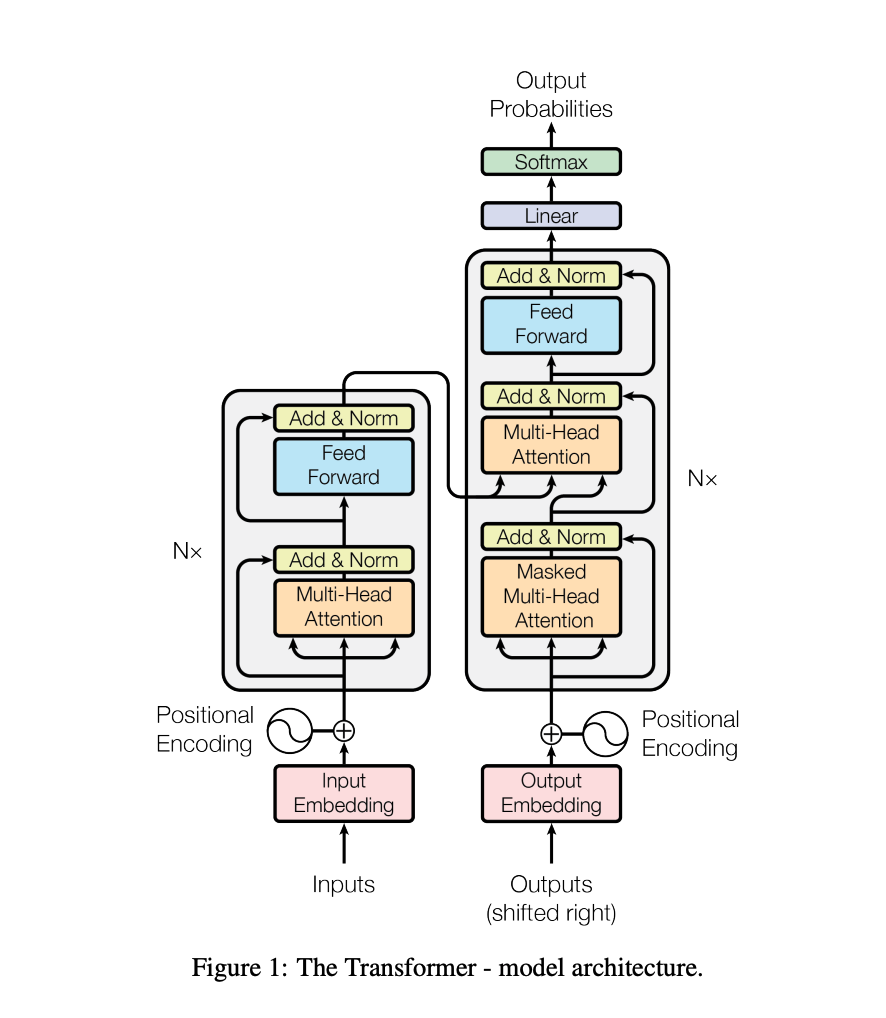
위 이미지를 보면 input과 output의 처리를 병렬적으로 진행할 수 있는데, 단계별로 다시 한번 살펴보자.
1단계 : 입력 단계
왼쪽 인코더
1. Inputs이 들어오면 임베딩과 위치 인코딩을 수행한다. (위치 인코딩은 sin, cos으로 계산한 값)
2. 임베딩 결과와 인코딩 값을 합친다.
오른쪽 디코더
1. shifted 된 문장을 임베딩하고, 위치 인코딩을 수행한다. (학습 시 right shift를 하는 이유는 이전 토큰들을 보고 다음 토큰을 예측해야 하기 때문이다. 추론 시에는 다음 토큰이 없으니 자연스럽게 shifted 되어있다.)
2. 임베딩 결과와 인코딩 값을 합친다.
2단계: 어텐션 학습 단계
왼쪽 인코더 스택 (Nx)
1. Multi-head Self-Attention을 수행한다.
2. 각 헤드를 concat하고 Linear Projection을 거쳐 출력한다.
3. 잔차 연결과 LayerNorm을 적용한다.
4. Feed Forward에 연결한다. 이를 통해 비선형성을 가지면서 표현력이 커진다.
- Linear Layer (확장) → ReLU → Linear Layer (축소)
5. 잔차 연결과 LayerNorm을 적용한다.
6. 위 과정을 N번 반복하여 인코더 최종 출력을 완성한다.
오른쪽 디코더 스택
1. Masked Multi-head Self-Attention을 진행한다. (학습 시 디코더가 미래의 토큰을 못보게 마스킹)
2. 각 헤드를 concat하고 Linear Projection을 거친 후, 잔차 연결과 LayerNorm을 적용한다.
3. Cross-Attention을 수행한다 (Query는 디코더의 현재 상태, Key/Value는 인코더의 출력을 활용한다.)
4. 잔차 연결과 LayerNorm을 적용한다.
5. Feed Forward에 연결한다.
6. 잔차 연결과 LayerNorm을 적용한다.
7. 위 과정을 N번 반복하여 디코더 최종 출력을 완성한다.
3단계 : 출력 단계
1. 디코더 최종 출력을 Linear Layer에 넣어 원하는 형태로 출력을 만든다.
2. Softmax에 넣고 최종 예측값을 출력한다.
학습 시에는 손실 계산과 역전파 과정을 통해 어텐션들을 학습시키고, 추론시에는 예측된 결과들만 출력한다. 트랜스포머 구조의 핵심 특징은 Residual Connection을 통해 정보 손실을 막고, Cross-Attention을 통해 성능을 극대화 한 것이다.
결론
트랜스포머는 기존 RNN이 가지는 구조적 한계를 해결해낸 혁신적인 아이디어이자 논문이다. 그 무거운 LSTM/GRU 를 사용하지 않고도 어텐션 구조를 만들었다는 것으로도 충분히 가치가 있는데, 각 레이어는 병렬적으로 동작하는데다 디코더도 동시에 학습을 시킬 수 있다는 점에서 엄청난 성능적 이점을 가져왔다.
특히, 컨텍스트 길이가 길어져도 모든 정보를 모델 내 인코더가 가지고 있기 때문에 정보 손실이 적고, 어텐션 계산에 있어 모델 크기보다 입/출력의 길이에만 영향을 받기 때문에 모델 크기에 대한 제약과 부담도 해소되었다고 볼 수 있다. (이전에는 모델이 커지면 hidden state가 커지고, 그걸 순차적으로 연산해야 했어서 무리였음)
이런 문제들을 해결하면서 효율적인 구조와 작은 모델들을 연구하던 패러다임을 완전히 뒤바꾸었는데, 이 논문이 나오고 그 다음해에 등장한 것이 117M 파라미터를 가지는 GPT-1 논문이다. (참고로 GPT는 2019년에는 1.5B, 2020년에는 175B까지... 폭발적으로 늘어난다)
그리고 더 무서운건, 트랜스포머가 등장한 이후로 트랜스포머만큼의 임팩트를 주는 아키텍처가 등장하지 않았었다는 사실이다. 오히려 이 아키텍처를 어떻게 잘 쓸지에 대한 연구들이 주류를 이루고 있다. 근데 왜 등장하지 않았었다라고 표현했냐면... 이번 2025 Google I/O 에서 큰 모델이 가지는 문제를 어느정도 해소한 구조를 가져왔기 때문이다. 아직 논문이 공개되진 않았는데 나오면 바로 해야지.
(그런데 이 구조가 학부생 시절 캡스톤하면서 장난으로 말했던 아이디어 중에 하나였는데, 이렇게 마주치니까 마음이 오묘하다...)

